Swap
FinPricing offers:
Four user interfaces:
- Data API.
- Excel Add-ins.
- Model Analytic API.
- GUI APP.
Swap Product and Valuation Guide
FinPricing covers various swaps, such as:
- Compounding Swap
- Basis Swap
- Vanilla Swap
- Amortizing Swap
- FRA
- Check FinPricing valuation models
An interest rate swap is an agreement between two parties to exchange future interest rate payments over a set of
future times. There are two legs associated with each party. Swaps are the most popular
OTC derivatives that are generally used to manage exposure to fluctuations in interest rates.
| 1. Interest Rate Swap Introduction |
An interest rate swap consists of a series of payment periods, called swaplets. The most popular form of interest rate swaps is the vanilla swaps that involve the exchange of a fixed interest rate for a floating rate, or vice versa. The swap only exchanges the interest but not principal. That is why the principal is called the notional principal. There are two legs associated with each party: a fixed leg and a floating leg. Swaps are OTC derivatives that bear counterparty credit risk beside interest rate risk.
Interest rate swaps are the most popular OTC derivatives that are generally used to manage exposure to fluctuations in interest rates. Swaps can be also used to obtain a marginally lower interest rate. Thus they are often utilized by a firm that can borrow money easily at one type of interest rate but prefers a different type. They also allow investors to adjust interest rate exposure and offset interest rate risks. Speculators use swaps to speculate on the movement of interest rates. More and more swaps are cleared through central counterparties nowadays (CCPs).
A standard or vanilla swap could be one of the following types: fixed-floating, floating-fixed, or floating-floating. A borrower with floating-rate debt who believes that interest rates are about to increase may enter into a swap agreement to pay fixed/receive floating. Similarly, a borrower with fixed-rate debt who believes that interest rates are about to fall may enter a swap agreement to pay floating/receive fixed.
A swap can be used to transform liability via so-called the comparative-advantage argument. One company can borrow a lower rate in fixed-rate markets, while the other company can borrow a lower rate in floating-rate markets. Consequently two companies can enter into a swap that benefits both. The swap will transform a floating-rate loa into a fixed-rate loan, and vice verse.
Swaps can also be used to mitigate risk and offset expsoure. For example, banks have a large number of exposure on fixed interest rate and floating interest rate. If the exposures can not offset each other. The remaining interest rate risk can be canceled out via interest rate swaps.
A swap is a financial vehicle for speculating on interest rate movement. To speculate an increase of interest rate, an investor will enter a swap that receives a floating rate and pays a fixed rate. Similarly, if he expects a fall of interest rate, he can enter a swap that pays a floating rate and receives a fixed rate.
Swaps help a company to lock an interest rate. For instance, an entity tries to issue a fixed rate bond, it typically lock in the current interest rate by entering into a swap for the issuing period. Once the bond is actually sold, they unwant the swap contract. The swap value will offset the interest rate changes during the selling period.
One of the partners to a swap may wish to terminate the agreement before it matures. If the present value of the contract is not zero at the time it is terminated, one partner will have to pay a termination fee to compensate the other.
| 2. Interest Rate Swap Valuation |
You may find different swap valuation models online: some just for intuitive understanding, some obsolete and others
not even correct. In this page, we elaborate the real-world model used in the market for calculating fair value and
risk.
A vanilla interest rate swap consists of a floating leg and a fixed leg. Here we simplify some notations in the model specification for brevity. More details are provided in practical notes for people who are interested in.
The present value of a fixed leg is given by
Practical Notes
- One of the most important factors for pricing a swap, including valuing a fixed leg, is to generate accurate cash flows. The generation is based on the start time, end time and payment frequency of the leg, plus calendar (holidays), business convention (e.g., modified following, following, etc.) and whether sticky month end.
- The accrual period or day count fraction is calculated according to the start date and end date of a cash flow plus day count convention
- Any compounded interest yield curves can be used to compute discount factor, of course the formulas will be slightly different. The most common used one is continuously compounded zero rates.
- Another fundamental factor is to construct interest zero curve by bootstrapping the most liquid interest rate instruments in the market. FinPricing provides useful tools to build various curves, such as interest rate swap curve, basis curve, OIS curve, bond curve, treasury curve, etc. Go to the list of the tools
The present value of a floating leg can be expressed as
Practical Notes
- All practical notes for pricing fixed leg are applicable to floating leg as well.
- To use the formula, you need to compute simply compounded forward rate instead of other compounding types.
- We assume that accrual periods are the same as reset periods and payment dates are the same as accrual end dates in the above formulas for brevity. But in fact, they are different due to different market conventions. For example, index periods can overlap each other but swap cash flows are not allowed to overlap.
- A forward rate should be computed based on the reset period (index reset date, index start date, index end date) that are determined by index definition, such as index tenor and convention.
- The formula above doesn’t contain the last live reset cash flow whose reset date is less than valuation date but payment date is greater than valuation date. The reset value isThe present value of the reset cash flow should be added into the present value of the floating leg.
The final present value of the swap is
Final practical notes
- Interest rate swaps are the most popular OTC derivatives. Most of them are either collateralized or cleared in the market. Therefore, pricing model should use OIS discounting to account for collateralization.
- Some dealers take bid-offer spreads into account. In this case, one should use bid curve constructed from bid quotes for forwarding and offer curve built from offer quotes for discounting.
Swap Rate and Swap Spread
A swap rate is the fixed rate that makes a given swap worth zero at inception.It can be easily derived from (1) and (2) as follows.
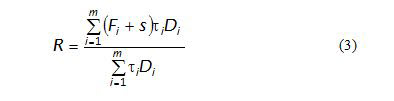
Swap spread is defined as the difference between a swap rate and the rate of an on-the-run treasury with the same maturity as the swap. The swap spread is the additional amount an investor would earn on a swap as compared to a risk-free fixed-rate investment.
| 3. Related Topics |
- 3.1 Interest Rate Basis Swap Valuation
- 3.2 Interest Rate Amortizing Swap or Accreting Swap Valuation
- 3.3 Compounding Swap Valuation
| 3.1 Interest Rate Basis Swap |
A basis swap is a swap where two parties exchange periodic floating rate payments. Both legs of a basis swap are floating but derived from different index rates (e.g. LIBOR 1 month vs 3 month).
The present value of leg 1 is given by
The present value of leg 2 can be expressed as
where the notations are the same as leg 1.
The final present value of the swap is
Practical notes
- Two floating legs are based on different indices, i.e., the forward curves are different. For example, leg 1 is forecasted by 1 month LIBOR curve and leg 2 is forecasted via 6 month swap curve data.
- Also the floating spreads s1 and s2 are different.
You can find more details at Interest Rate Basis Swap
| 3.2 Interest Rate Amortizing Swap or Accreting Swap |
An amortizing swap is an interest rate swap whose notional principal amount declines during the life of the contract whereas an accreting swap is an interest rate swap whose notional principal amount increases instead. The notional amount changes could be one leg or two legs. To be generic, we assume that the notional amount changes apply to both legs. The analytics are similar to a vanilla swap except the national amount used per period may be different.
The present value of a fixed leg is given by
The present value of a floating leg can be expressed as
The final present value of the swap is
Practical notes
- All practical notes for pricing a regular vanilla swap are applicable to amortizing swap or accreting swaps.
- You need to determine notional principal amount for each cash flow when you generate it.
You can find more details at Interest Rate Amortizing and Accreting Swap
| 3.3. Compounding Swap |
A compounding swap consists of two legs: a regular fixed leg and a compounding leg. The compounding leg is similar to a regular floating leg except the reset frequency is higher than the payment frequency. For example, a compounding leg has 1 month reset frequency and 3 month payment frequency. The most popular compounding swap is Overnight Indexed Swap (OIS).
The present value of a compounding leg is given by
Here we assume that there are k reset periods within the i-th cash flow.
The present value of the fixed leg is the same as (1)
The final present value of the swap is
Practical notes
- All practical notes for pricing a regular vanilla swap are applicable to compounding swaps.
- You also need to generate reset flows within each cash flow.
| References |