Amortizing Swap
FinPricing offers:
Four user interfaces:
- Data API.
- Excel Add-ins.
- Model Analytic API.
- GUI APP.
Amortizing Swap Valuation
An interest rate swap is an agreement between two parties to exchange future interest rate
payments over a set of future times. There are two legs associated with each party. Swaps
are the most popular OTC derivatives that are generally used to manage exposure to fluctuations in interest rates.
| 1. Amortizing and Accreting Swap Introduction |
An amortizing swap is an interest rate swap whose notional principal amount declines
during the life of the contract whereas an accreting swap is an interest rate swap whose
notional principal amount increases instead. The notional amount changes could be one leg or two legs, but typically
on a fixed schedule. The notional principal is tied to an underlying financial instrument with a declining principal,
such as a mortgage or an increasing principal, such as a construction fund.
The notional principal of an amortizing swap is tied to an underlying financial instrument with a declining principal,
such as a mortgage. On the other hand, the notional amount of an accreting swap is tied to an underlying instrument
with an increasing principal, such as a construction fund. The notional principal schedule of an amortizing or an
accreting swap may decrease or increase at the same rate as the underlying instrument. Both amortizing and accreting
swaps can be used to reduce or increase exposure to fluctuations in interest rates.
| 2. Amortizing and Accreting Swap Valuation |
You may find different swap valuation models online: some just for intuitive understanding,
some obsolete and others not even correct. In this page, we elaborate the real-world model used in the market for
calculating fair value and risk.
An amortizing swap is an interest rate swap whose notional principal amount declines during the life of the contract whereas an accreting swap is an interest rate swap whose notional principal amount increases instead. The notional amount changes could be one leg or two legs. To be generic, we assume that the notional amount changes apply to both legs. The analytics are similar to a vanilla swap except the national amount used per period may be different.
The present value of a fixed leg is given by
The present value of a floating leg can be expressed as
The final present value of the swap is
Practical Notes
- One of the most important factors for pricing a swap is to generate accurate cash flows. The generation is based on the start time, end time and payment frequency of the leg, plus calendar (holidays), business convention (e.g., modified following, following, etc.) and whether sticky month end.
- The accrual period or day count fraction is calculated according to the start date and end date of a cash flow plus day count convention
- Any compounded interest yield curves data can be used to compute discount factor, of course the formulas will be slightly different. The most common used one is continuously compounded zero rates.
- Another fundamental factor is to construct yield curve by bootstrapping the most liquid interest rate instruments in the market. FinPricing provides useful tools to build various curves, such as swap curve, basis curve, OIS curve, bond curve, treasury curve, etc. Go to the list of the tools
- To use the formula, you need to compute simply compounded forward rate instead of other compounding types.
- We assume that accrual periods are the same as reset periods and payment dates are the same as accrual end dates in the above formulas for brevity. But in fact, they are different due to different market conventions. For example, index periods can overlap each other but swap cash flows are not allowed to overlap.
- A forward rate should be computed based on the reset period (index reset date, index start date, index end date) that are determined by index definition, such as index tenor and convention.
- The formula above doesn’t contain the last live reset cash flow whose reset date is less than valuation date but payment date is greater than valuation date. The reset value isThe present value of the reset cash flow should be added into the present value of the floating leg.
- You need to determine notional principal amount for each cash flow when you generate it.
| 3. Related Topics |
- 3.1 Interest Rate Basis Swap Valuation
- 3.2 Interest Rate Vanilla Swap Valuation
- 3.3 Compounding Swap Valuation
| 3.1 Interest Rate Basis Swap |
A basis swap is a swap where two parties exchange periodic floating rate payments. Both legs of a basis swap are floating but derived from different index rates (e.g. LIBOR 1 month vs 3 month).
The present value of leg 1 is given by
The present value of leg 2 can be expressed as
where the notations are the same as leg 1.
The final present value of the swap is
Practical notes
- Two floating legs are based on different indices, i.e., the forward curves are different. For example, leg 1 is forecasted by 1 month LIBOR curve and leg 2 is forecasted via 6 month LIBOR curve data.
- Also the floating spreads s1 and s2 are different.
You can find more details at Interest Rate Basis Swap
| 3.2 Interest Rate Vanilla Swap |
A vanilla interest rate swap consists of a floating leg and a fixed leg. Here we simplify some notations in the model specification for brevity. More details are provided in practical notes for people who are interested in.
The present value of a fixed leg is given by
The present value of a floating leg can be expressed as
The final present value of the swap is
Swap Rate and Swap Spread
A swap rate is the fixed rate that makes a given swap worth zero at inception.It can be easily derived from (1) and (2) as follows.
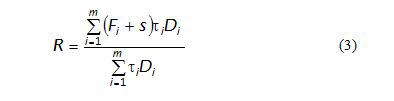
Swap spread is defined as the difference between a swap rate and the rate of an on-the-run treasury with the same maturity as the swap. The swap spread is the additional amount an investor would earn on an interest rate swap as compared to a risk-free fixed-rate investment.
Final practical notes
- Interest rate swaps are the most popular OTC derivatives. Most of them are either collateralized or cleared in the market. Therefore, derivative pricing model should use OIS discounting to account for collateralization.
- Some dealers take bid-offer spreads into account. In this case, one should use bid curve constructed from bid quotes for forwarding and offer curve built from offer quotes for discounting.
You can find more details at Interest Rate Vanilla Swap
| 3.3. Compounding Swap |
A compounding swap consists of two legs: a regular fixed leg and a compounding leg. The compounding leg is similar to a regular floating leg except the reset frequency is higher than the payment frequency. For example, a compounding leg has 1 month reset frequency and 3 month payment frequency. The most popular compounding swap is Overnight Indexed Swap (OIS).
The present value of a compounding leg is given by
Here we assume that there are k reset periods within the i-th cash flow.
The present value of the fixed leg is the same as (1)
The final present value of the swap is
Practical notes
- All practical notes for pricing a regular vanilla swap are applicable to compounding swaps.
- You also need to generate reset flows within each cash flow.
You can find more details at Interest Rate Compounding Swap
| References |