Callable Bond


FinPricing offers:

Four user interfaces:

  • Data API.
  • Excel Add-ins.
  • Model Analytic API.
  • GUI APP.
View:

Callable Bonds Valuation


FinPricing provides probably the most comprehensive valuation models for financial products, including computation of:


The models calculate clean price, dirty price, accrual interest, yield to maturity, yield to call, yield to best, and yield to worst.


1. Callable Bond Introduction

A callable bond is a bond in which the issuer has the right to call the bond at specified times from the investor for a specified price.

At each callable date prior to the bond maturity, the issuer may recall the bond from its investor by returning the investor’s money. The underlying bonds can be fixed rate bonds or floating rate bonds. A callable bond can therefore be considered a vanilla underlying bond with an embedded style Bermudan style option. Callable bonds protect issuers. Therefore, a callable bond normally pays the investor a higher coupon than a non-callable bond.

Although a callable bond is a higher cost to the issuer and an uncertainty to the investor comparing to a regular bond, it is actually quite attractive to both issuers and investors. For issuers, callable bonds allow them to reduce interest costs at a future date should rate decrease. For investors, callable bonds allow them to earn a higher interest rate of return until the bonds are called off. This presentation gives an overview of callable bond and valuation model. Click the links below for details.


2. Callable Bond Payoffs

Assume that the maturity of a fixed rate callable bond is T. there are n call dates denoted as .

The payoff of a callable bond at maturity is given by

Callable bond payoff in FinPricing

The payoff of the callable bond at any call date T_i is given by

Callable bond valuation in FinPricing

3. Valuation Model Selection Criteria

Given the complexity of callable bond valuation, there is no closed form solution. Therefore, we need to select an interest rate term structure model and a numeric solution to price Bermudan swaptions.

Popular IR term structure models in the market are Hull-White, Linear Gaussian Model (LGM), Quadratic Gaussian Model (QGM), Heath Jarrow Morton (HJM), Libor Market Model (LMM). HJM and LMM are too complex while Hull-White is inaccurate for computing sensitivities. Therefore, we choose either LGM or QGM.

After selecting a term structure model, we need to choose a numeric approach to approximate the underlying stochastic process of the model.Commonly used numeric approaches are tree, partial differential equation (PDE), lattice, and Monte Carlo simulation. Tree and Monte Carlo are notorious for inaccuracy in sensitivity calculation. Therefore, we choose either PDE or lattice. Our final decision is to use LGM plus lattice.


4. LGM Model
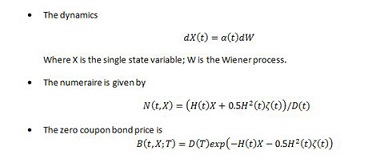
Linear Gaussian Model (LGM) in FinPricing

5. LGM Assumptions and Calibration

The LGM model is mathematically equivalent to the Hull-White model but offers significant improvements in calibration stability and accuracy. It is also more accurate and stable in sensitivity calculation. The state variable is normally distributed under the appropriate measure. The LGM model has only one stochastic driver (one-factor), thus changes in rates are perfected correlated.

At time t, X(0)=0 and H(0)=0. Thus Z(0,0;T)=D(T). In other words, the LGM automatically fits today’s discount curve or yield curve. To calibrate swaption implied volatilities, first select a group of market swaptions and then solve parameters by minimizing the relative error between the market swaption prices and the LGM model swaption prices.


5. Valuation Practical Guide
  • Calibrate the LGM model first.
    • <
  • Create the lattice based on the LGM: the grid range should cover at least 3 standard deviations.
  • Find the underlying bond value at each final note.
  • Conduct backward induction process iteratively rolling back from final dates until reaching the valuation date.
  • Compare exercise values with intrinsic values at each exercise date.
  • The value at the valuation date is the price of the callable bond.
  • Check Callable exotics.

References