FVA
FinPricing offers:
Four user interfaces:
- Data API.
- Excel Add-ins.
- Model Analytic API.
- GUI APP.
| 1. FVA Introduction |
Financial institutions used to disregard, or at least minimize, credit and funding costs. Historically, the funding for taking on in-the-money trades and for posting collateral could be achieved through a variety of low cost funding options and this low cost was to some extent offset by the interest paid on collateral by the receiving party.
The financial crisis has changed this view as funding has become more costly, and the interest paid on collateral no longer offsets the increased cost. The evaluation and controlling of funding costs have therefore become a critical part of the risk management strategy of financial institutions. Thus, some adjustments has been introduced to the valuation of a derivative contract to account for counterparty and funding risk.
. On the funding risk side, a funding cost or benefit can be incurred during the lifetime of the uncollateralized derivative transactions, leading to a Funding Valuation Adjustment (FVA). FVA is an adjustment to the value of a derivative or a derivatives portfolio to ensure that a trader recovers a funding costs/benefit that is consistent with the market’s view of the funding costs/benefits associated with the same trade.
The rationale for the adjustment is that in executing the derivative, a bank may be committing itself to future funding requirements (or benefits). In certain constructs, the derivatives desk of a bank may be charged the bank’s average funding cost by an internal funding desk.
An uncollateralized trade may require a funding value adjustment, which is a loss, in order to account for the market’s view of funding costs associated with the trade. For trades that generate funding, such as the sale of options, an FVA is a benefit because such trades reduce the external funding requirements of a bank.
FVA is introduced to capture the incremental costs of funding uncollateralized derivatives. It can be referred to as
the difference between the rate paid for the collateral to the bank’s treasury and rate paid by the clearinghouse.
Also FVA can be thought of as a hedging cost or benefit arising from the mismatch between an uncollateralized client
trade and a collateralized hedge in the interdealer market. FVA should be also calculated at portfolio level.
| 2. FVA Calculation |
FCA can be calculated based on the incremental spread over and above the counterparty’s CDS spreads to bring the all-in spread to a level that is consistent with where bonds issued by the counterparty are priced in the market. That is, where the counterparty borrows provides an indication of the price of credit and funding according to its lenders.
FBA can be calculated based on the incremental spread over and above the bank’s CDS spreads to bring the all-in spread to a level that is consistent with where the bank’s bonds are priced in the market.
If asset side bond spreads are below your own bond issuance costs, a liquidity premium topping up the bond spread to match your cost of funds will be added. This is essentially a lending floor set to your funding levels. Counterparties with low bond spreads often have very liquid debt supported by the repo market. Since derivative assets are not fundable in the repo market this premium is an important adjustment to prevent underfunding derivative assets.
We expect to recover the standard result that the FVA is simply the difference between the risk-free and risky loan values. We compute FVA using the same framework as CVA and find the cost of protecting a loan against counterparty default effectively introduces a spread which compensates the lender for taking on the borrower’s default risk. We show that under general conditions a loan’s CVA can be approximated as the discounted value of the notional principle, bond or CDS spread, and time to maturity.
Consider an agreement between two counterparties to borrow a unit sum at t = 0, to be repaid at a future time t = T. Assume the loan accrues interest at the par floating rate r plus a spread s. The spread will be chosen to fairly compensate the lender for assuming the borrower’s credit risk for the duration of the loan. We compute FVA using the above notation. The price of the credit-risk-free loan at an arbitrary earlier time is
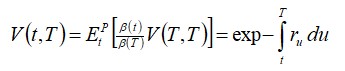
or simply the time-t value of a certain dollar received at later time T, as expected. The loan value under credit risk follows as

Again, we use standard notation and denote default as a Bernoulli process with default time τ, recovery rate R and default intensity λ. We have also assumed the default and interest rate processes are independent so the expectation can be decoupled into a product. This shows the loan’s value under credit risk is lower than the risk-free case, as expected the lender has to be compensated for assuming the borrower’s credit risk. In practice the lender charges an interest rate above the risk-free rate.
This relates the compensation the lender requires to the recovery rate and the default intensity (and hence the default probability) of the borrower. These are usually obtained through either the corporate bond or the credit default swap markets. In an ideal world with infinite liquidity and perfect price discovery we can argue that the probability of default and expected recovery for any specific issuer should be the same whether inferred from bond prices or from CDS spreads.
In practice however the two markets are not perfectly coupled and we have to recognize a basis between estimates made in the two markets, to take into account differing liquidity and views on seniority of any particular issue. Some evidence indicates CDS leads the bond market in signally market changes. In the case above, the bullet loan is essentially a zero coupon bond, and the bond market is the relevant one for calibrating recovery and default probability.
| 3. Related Topics |