Futures
FinPricing offers:
Four user interfaces:
- Data API.
- Excel Add-ins.
- Model Analytic API.
- GUI APP.
An interest rate futures is a futures contract between the buyer and seller to deliver an interest bearing asset,
that allows the buyer and seller to lock in the price of the interest bearing asset for a future date. The most
popular interest rate futures is Eurodollar futures.
| 1. Futures Introduction |
Eurodollar futures contract is a cash-settled futures contract. The underlying instrument in Eurodollar futures is a
Eurodollar time deposit having a principal value of $1,000,000 with a three-month maturity. Eurodollar futures prices
are expressed numerically using 100 minus the implied 3-month U.S. LIBOR interest rate. In this way, a Eurodollar
future price of $98 reflects an implied settlement interest rate of 2%.
Interest rate futures are used to hedge against interest rate risk. Investors can use Eurodollar futures to secure
interest rates for money it plans to borrow or lend in the future.
| 2. Futures Valuation |
The price of an interest rate future is quoted by the exchange. Thus, a model is mainly used for calculating sensitivities and managing market risk. The present value of an IR future contract is given by
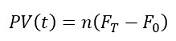
Practical Notes
| References |