Quanto Option
FinPricing offers:
Four user interfaces:
- Data API.
- Excel Add-ins.
- Model Analytic API.
- GUI APP.
FinPricing provides valuation models for:
| 1. Quanto Option Introduction |
A quanto option is an instrument where two currencies are involved. The payment is determined in one currency and paid in the other currency. For example, a quanto option that provides a payoff in currency EUR at time T. But payoff depends on the value of a stock MSFT that is defined in currency USD at time T.
Quanto derivatives are quite common. The types of financail contracts with quanto features in practice are wide, encompassing futures, forwards, vanilla options and exotic notes.
Quanto contract allows investors to invest their money in foreign market without exchange rate risk. As such, it gives people opportunity to participate in the return of international markets without the foreign exchange risk exposure.
Quanto optionality is attractive to investors because it is able to remove currency risk for oversea investment. Many exotic options and notes have quato features that benefit from the price appreciation of foreign markets and also shield exchange rate variations.
| 2. Quanto Option Valuation |
Quanto-adjustment technique approximates the equity price process by a geometric Brownian motion and then adjusts the foreign currency risk-free interest rate curve, by adding a spread based on the product of the following parameter values:
The currency in which a quanto option is settled when exercised is called domestic currency. The foreign currency is the currency in which the option's underlying is denominated. The domestic currency must be different from the foreign currency in the case of quanto option.
Let S be the stock price measured in a foreign currency paying a (continuous) dividend yield q. Let X be the foreign exchange (FX) rate, domestic currency per one unit of foreign currency. The risk-neutral process for S under foreign risk-neutral measure is
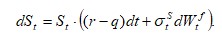
Under domestic risk-neutral measure it becomes (by applying change-of-numeraire technique):
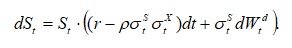
This equation comes from the application of Girsanov theorem to translate from the risk-neutral probability in foreign currency to the risk-neutral probability measure in domestic currency.
The quanto forward for maturity T as seen at time t is then:
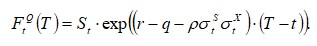
The forward quanto price under dividend yield is given by:
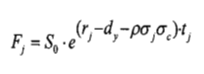
The forward quanto price under discrete dividend is given by:
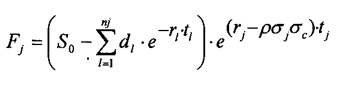
The formula tells us that a forward quanto price is equal to a normal forward price multiplied by a quanto correction.
The price of a quanto call option is
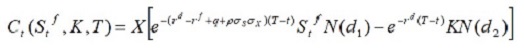
The price of a quanto put option is
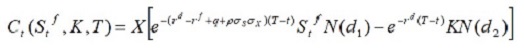
| 3. Related Topics |