Variance Swap
FinPricing offers:
Four user interfaces:
- Data API.
- Excel Add-ins.
- Model Analytic API.
- GUI APP.
Variance Swap Valuation
FinPricing provides valuation models for:
- Variance Swap
- Index Variance Swap
- Variance Swap with Caps and Floors
- Volatility Swap with Convexity Adjustment
- Feldmex Variance Swap
- Bitcoin Variance Swap
- Check FinPricing valuation models
| 1. Variance Swap Introduction |
A variance swap is an instrument that allows explicit exposure to the realized variance of an asset without exposure to other risks commonly encountered with derivatives. Investors can use variance swap to trade future realized (historical) variance against current implied variance. In other words, the payoff of a variance is based on the difference between a variance level specified when the contract is initiated, and the “realized” variance during the life of the contract.
The observed variance is computed from the stock price returns over a series of specified sampling dates. The unrealized variance forecast is obtained by integrating the replicated portfolio of vanilla European options with infinite number of strikes. There are no intermediate payments; the only payment occurs at maturity.
The market value of a variance swap is based on the variance determined from a combination of realized (historical) variance and unrealized variance, possibly subject to a cap and a floor.
| 2. Variance Swap Payoffs |
The Variance Swap pays the difference between observed variance and a strike variance. The initial Variance level specified in the swap is referred to as the strike level. Let K denote the strike level in variance swap. At maturity a variance swap has the following payoff:
| 3. Volatility Swap Introduction |
A volatility swap is a derivative that allows investors to trade future realized volatility against current implied volatility. The volatility Swap pays the difference between observed volatility and a strike volatility, possibly subject to a cap and a floor. The observed volatility is computed from the stock price returns over a series of specified sampling dates.
At maturity a volatility swap has the following payoff:
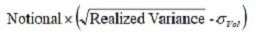
| 4. Variance Swap Valuation |
A Variance Swap contract has a payoff that is dependent on realized variance. In order to calculate the fair value of future delivery variance, the variance swap can be replicated by a portfolio of European call and put options with a continuous range of strikes. This continuous spectrum of options is not observable and hence a finite discrete approximate replication is performed in practice.
It should be aware that the replication portfolio is derived under assumptions of existence of a perfect replication portfolio comprised of an infinite number of vanilla call/put options. In reality, the replication portfolio will only have finite number of call & put options within a certain strike range.
Usually, the model assumes continuous underlying evolution, while in reality the underlying can jump. The replication portfolio then may no longer capture the realized volatility and this may lead to the replication error. As such, it may distort the accuracy of the hedging and risk measurement.
The present value of a variance swap is given by:
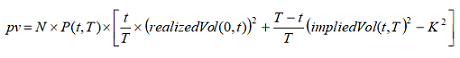
| 5. Volatility Swap Valuation |
To value a volatility swap, one needs to compute releazed variance and future variance first as describled above. Then compute volatility as then squre root of variance. Since the payoff and valuation of volatility swap has nonlinear square root, a convexity adjustment is required.
| Related Topics |